什么是并查集

并查集是一种十分简单的数据结构，它可以用来描述元素的分组情况。
并查集可以十分高效地进行“并”和“查”两个操作，但无法进行分割操作。
其中：

并：合并a，b两个元素所在的组；
查：查询a，b两个元素是否属于同一组；

并查集的本质是一棵棵树的合并，以及树的遍历。

并查集的结构

并查集是一种树形结构（并非二叉树），使用并查集后，多数情况下会有不止一棵树，即一个森林。

初始化

在初始状态时，所有元素均和自己且只和自己是一组，这是毋庸置疑的。

并查集作为一个树形结构，我们需要有一个根节点用来描述一棵树，这里，我们定义一个“par数组”来描述这个根节点。

在初始化时，需要设定：

par[i] = i;

初始化

合并

现在给出信息：

1和4一组
2和3一组
1和3一组
5和6一组

对于给出的四条信息，我们依次进行操作：

由于1和4一组，我们约定：左侧节点作为根节点，因此，我们将par[4]更新为1；
由于2和3一组，根据靠左原则，将par[3]更新为2；
当遇见“1和3一组”这条信息时，我们发现2和3一组，如果贸然将par[3]更新为1，就不满足2和3一组的条件；为同时保证2和3一组的条件，我们需要找到它的根节点并将其根节点与另一节点合并（即2，并将2和1合并），此时将par[2]更新为1，如此便可以满足2和3一组的同时1和3也处于同一组。
由于5和6一组，根据靠左原则，将par[6]更新为5；

（在第三步中，在找到其根节点的过程中，可以将其路径上的所有节点par直接更新为根节点，这个操作称为路径压缩，此示例没有体现）
如此，我们可以得到如下图所示的森林：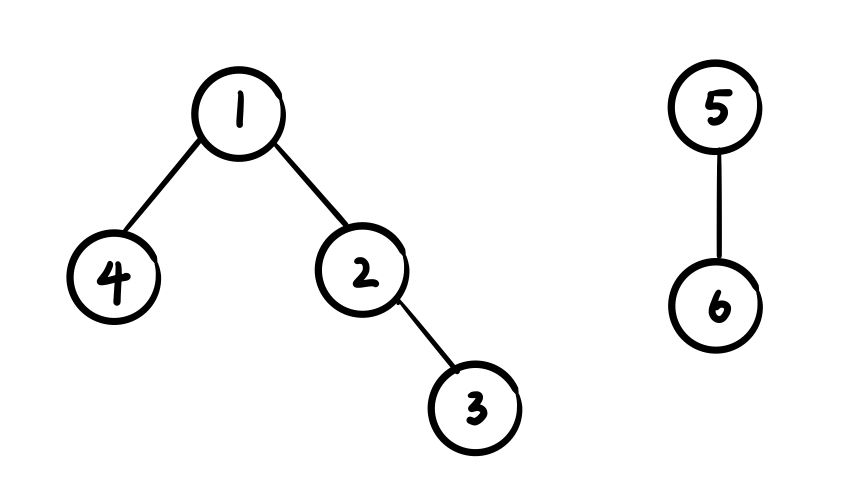
合并操作

查询

为了查询两个节点是否属于同一组，我们需要沿着树向上走，以此来查询包含这个元素的根节点是谁；如果两个节点走到了同一个根节点，那么我们就可以知道他们属于同一组。
假设现在查询3和4是否处于同一组中，我们需要：

找到4的根节点：1
找到3的根节点：1
2.1.在此过程中，3先找到其父节点2，发现2并非根节点，再向上寻找发现1为根节点，此过程中可以将2和3的par都更新为1
可以发现3和4的根节点都是1，说明他们属于一个集合

实现

初始化

void init (int n){
    for (int i = 0;i < n; i++){
        par[i] = i;
    }
}

查询树的根节点

在合并和查询时，我们都需要找到其根节点：

如果此节点是单个节点，即par[x] == x，就说明它是根节点
否则，判断par[x]是否为根节点，直至找到根节点为止

如此可以得到如下函数：

int getf(int x)
{
    if(par[x] == x){
        return x;
    }
    else {
     return par[x] = getf(par[x]);//这里用到了路径压缩操作     
    }
}

或者可以简写成如下形式：

int getf(int x){
    return par[x] == x ? x : par[x] = getf(par[x]);
}

合并

void unite(int x,int y)
{
    x=getf(x);
    y=getf(y);
    if(x!=y){
        par[y]=x;
    }
}

查询

bool query(int x, int y){
    return getf(x) == getf(y);    
}

再谈并查集

再优化

在对树的学习中，我们知道，当一棵树退化成链时，其效率是非常低的，因此我们要对树的层数进行平衡。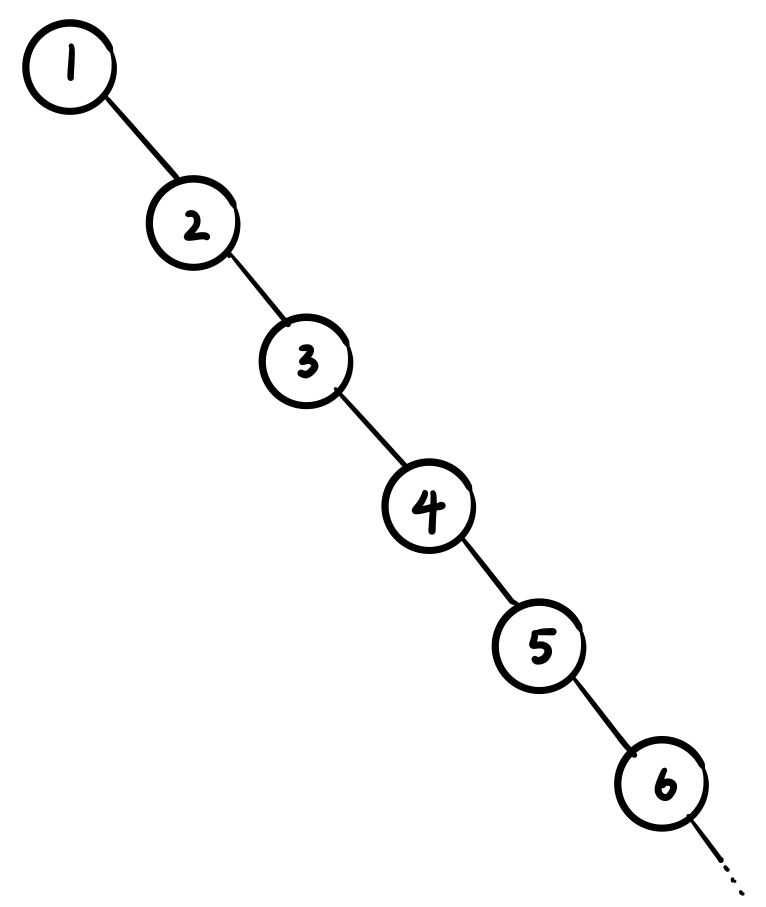
在这里插入图片描述

如此一来，我们需要额外多维护一个树的高度（rank）。
合并时，如果两棵树的rank不同，则不遵循靠左原则，从rank小的树向rank大的树连边
这样，我们可以得到最终的初始化和合并函数：

void init (int n){
    for (int i = 0;i < n; i++){
        par[i] = i;
        rank[i] = 0;
    }
}
void unite(int x,int y){
    x = getf(x);
    y = getf(y);
    if (x == y){
        return;
    }
    if (rank[x] < rank[y]){
        par[x] = y;
    }
    else{
        par[y] = x;
        if (rank[x] == rank[y]){
            rank[x]++;
        }
    }
}

并查集的时间复杂度

在避免了树的退化的同时加入路径压缩操作，并查集的效率非常高，其均摊复杂度为：
Θ ( α ( n ) ) \Theta(\alpha(n)) Θ(α(n))，其中 α ( n ) \alpha(n) α(n)为阿克曼函数的反函数，此效率比 Θ ( log ⁡ ( n ) ) \Theta(\log(n)) Θ(log(n))还要高。