决策树-向日葵屋

决策树

熵的定义

计算给定数据集的熵

def calcShannonEnt(dataSet):
    numEntires = len(dataSet)                        #返回数据集的行数
    labelCounts = {}                                #保存每个标签(Label)出现次数的字典
    for featVec in dataSet:                            #对每组特征向量进行统计
        currentLabel = featVec[-1]                    #提取标签(Label)信息
        if currentLabel not in labelCounts.keys():    #如果标签(Label)没有放入统计次数的字典,添加进去
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1                #Label计数
    shannonEnt = 0.0                                #经验熵(香农熵)
    for key in labelCounts:                            #计算香农熵
        prob = float(labelCounts[key]) /numEntires
        #选择该标签(Label)的概率
        shannonEnt -= prob * log(prob, 2)            #利用公式计算
    return shannonEnt                                #返回经验熵(香农熵)

数据集格式

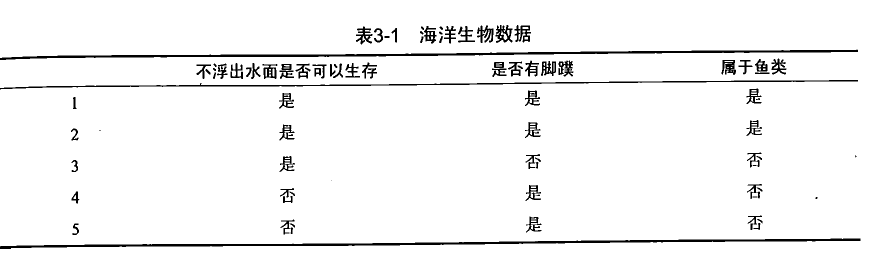
def createDataSet():
    dataSet=[[1,1,'yes'],[1,1,'yes'],[1,0,'no'],[0,1,'no'],[0,1,'no']]
    labels=['no surfacing','flippers']
    return dataSet,labels

进行测试计算，添加了第三个名为maybe的分类，熵增加。（熵越高，则混合的数据越多）

from decisionTree import *
myDat,labels=createDataSet()
print(myDat)
print(labels)
print(calcShannonEnt(myDat))
myDat[0][-1]='maybe'
print(myDat)
print(calcShannonEnt(myDat))

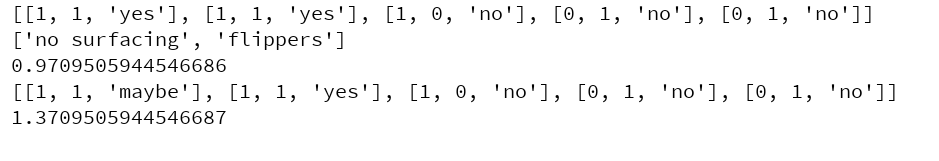
按照给定特征划分数据集

def splitDataSet(dataSet, axis, value):
    retDataSet=[]
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec=featVec[:axis]
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet

测试及结果

print(splitDataSet(myDat,0,1))
#[[1, 'maybe'], [1, 'yes'], [0, 'no']]
print(splitDataSet(myDat,0,0))
#[[1, 'no'], [1, 'no']]
def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1                    #特征数量
    baseEntropy = calcShannonEnt(dataSet)                 #计算数据集的香农熵
    bestInfoGain = 0.0                                  #信息增益
    bestFeature = -1                                    #最优特征的索引值
    for i in range(numFeatures):                         #遍历所有特征
        #获取dataSet的第i个所有特征
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)                         #创建set集合{},元素不可重复
        newEntropy = 0.0                                  #经验条件熵
        for value in uniqueVals:                         #计算信息增益
            subDataSet = splitDataSet(dataSet, i, value)         #subDataSet划分后的子集
            prob = len(subDataSet) / float(len(dataSet))           #计算子集的概率
            newEntropy += prob * calcShannonEnt(subDataSet)     #根据公式计算经验条件熵
        infoGain = baseEntropy - newEntropy                     #信息增益
        print("第%d个特征的增益为%.3f" % (i, infoGain))            #打印每个特征的信息增益
        if (infoGain > bestInfoGain):                             #计算信息增益
            bestInfoGain = infoGain                             #更新信息增益，找到最大的信息增益
            bestFeature = i                                     #记录信息增益最大的特征的索引值
    return bestFeature                                             #返回信息增益最大的特征的索引值