【深度学习】BP反向传播算法Python简单实现

妖狐艹你老母 2022-06-05 11:09 287阅读 0赞

  个人觉得BP反向传播是深度学习的一个基础，所以很有必要把反向传播算法好好学一下
  得益于一步一步弄懂反向传播的例子这篇文章，给出一个例子来说明反向传播
  不过是英文的，如果你感觉不好阅读的话，优秀的国人已经把它翻译出来了。
  一步一步弄懂反向传播的例子（中文翻译）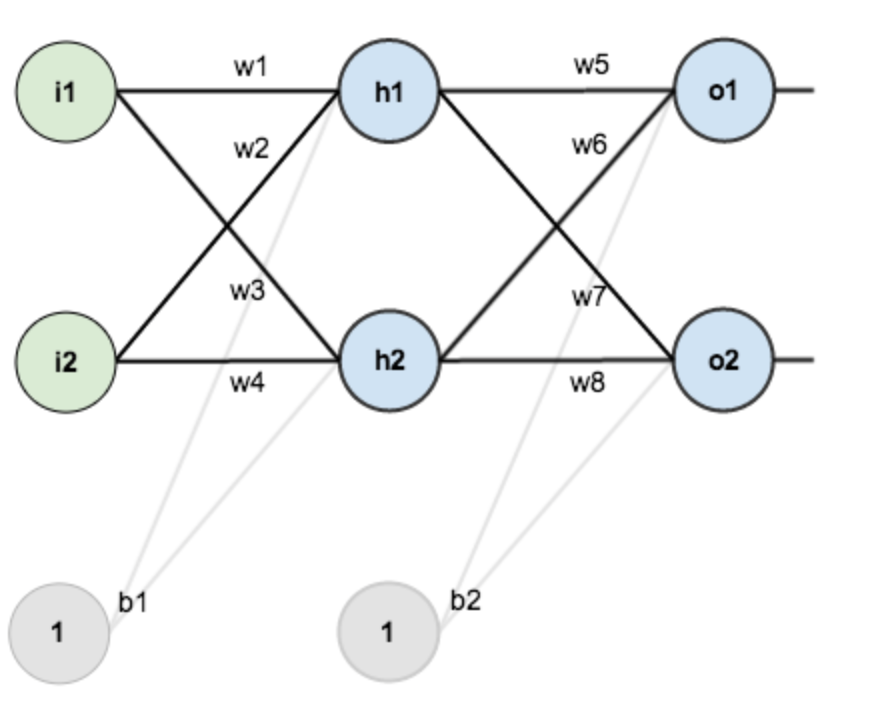
神经网络
  然后我使用了那个博客的图片。这次的目的主要是对那个博客的一个补充。但是首先我觉得先用面向过程的思想来实现一遍感觉会好一点。随便把文中省略的公式给大家给写出来。大家可以先看那篇博文。

∂Etotal∂w5=∂Etotal∂outo1×∂outo1∂neto1×∂neto1∂w5∂Etotal∂w6=∂Etotal∂outo1×∂outo1∂neto1×∂neto1∂w6∂Etotal∂w7=∂Etotal∂outo2×∂outo2∂neto2×∂neto2∂w7∂Etotal∂w8=∂Etotal∂outo2×∂outo2∂neto2×∂neto2∂w8∂Etotal∂w1=∂Etotal∂outh1×∂outh1∂neth1×∂neth1∂w1∂Etotal∂w2=∂Etotal∂outh1×∂outh1∂neth1×∂neth1∂w2∂Etotal∂w3=∂Etotal∂outh2×∂outh2∂neth2×∂neth2∂w3∂Etotal∂w4=∂Etotal∂outh2×∂outh2∂neth2×∂neth2∂w4(1)(2)(3)(4)(5)(6)(7)(8) (1) ∂ E t o t a l ∂ w 5 = ∂ E t o t a l ∂ o u t o 1 × ∂ o u t o 1 ∂ n e t o 1 × ∂ n e t o 1 ∂ w 5 (2) ∂ E t o t a l ∂ w 6 = ∂ E t o t a l ∂ o u t o 1 × ∂ o u t o 1 ∂ n e t o 1 × ∂ n e t o 1 ∂ w 6 (3) ∂ E t o t a l ∂ w 7 = ∂ E t o t a l ∂ o u t o 2 × ∂ o u t o 2 ∂ n e t o 2 × ∂ n e t o 2 ∂ w 7 (4) ∂ E t o t a l ∂ w 8 = ∂ E t o t a l ∂ o u t o 2 × ∂ o u t o 2 ∂ n e t o 2 × ∂ n e t o 2 ∂ w 8 (5) ∂ E t o t a l ∂ w 1 = ∂ E t o t a l ∂ o u t h 1 × ∂ o u t h 1 ∂ n e t h 1 × ∂ n e t h 1 ∂ w 1 (6) ∂ E t o t a l ∂ w 2 = ∂ E t o t a l ∂ o u t h 1 × ∂ o u t h 1 ∂ n e t h 1 × ∂ n e t h 1 ∂ w 2 (7) ∂ E t o t a l ∂ w 3 = ∂ E t o t a l ∂ o u t h 2 × ∂ o u t h 2 ∂ n e t h 2 × ∂ n e t h 2 ∂ w 3 (8) ∂ E t o t a l ∂ w 4 = ∂ E t o t a l ∂ o u t h 2 × ∂ o u t h 2 ∂ n e t h 2 × ∂ n e t h 2 ∂ w 4 

  1. import numpy as np
  3. # "pd" 偏导
  4. def sigmoid(x):
  5.     return 1 / (1 + np.exp(-x))
  6. def sigmoidDerivationx(y):
  7.     return y * (1 - y)
  9. if __name__ == "__main__":
  10.     #初始化
  11.     bias = [0.35, 0.60]
  12.     weight = [0.15, 0.2, 0.25, 0.3, 0.4, 0.45, 0.5, 0.55]
  13.     output_layer_weights = [0.4, 0.45, 0.5, 0.55]
  14.     i1 = 0.05
  15.     i2 = 0.10
  16.     target1 = 0.01
  17.     target2 = 0.99
  18.     alpha = 0.5 #学习速率
  19.     numIter = 90000 #迭代次数
  20.     for i in range(numIter):
  21.         #正向传播
  22.         neth1 = i1*weight[1-1] + i2*weight[2-1] + bias[0]
  23.         neth2 = i1*weight[3-1] + i2*weight[4-1] + bias[0]
  24.         outh1 = sigmoid(neth1)
  25.         outh2 = sigmoid(neth2)
  26.         neto1 = outh1*weight[5-1] + outh2*weight[6-1] + bias[1]
  27.         neto2 = outh2*weight[7-1] + outh2*weight[8-1] + bias[1]
  28.         outo1 = sigmoid(neto1)
  29.         outo2 = sigmoid(neto2)
  30.         print(str(i) + ", target1 : " + str(target1-outo1) + ", target2 : " + str(target2-outo2))
  31.         if i == numIter-1:
  32.             print("lastst result : " + str(outo1) + " " + str(outo2))
  33.         #反向传播
  34.         #计算w5-w8(输出层权重)的误差
  35.         pdEOuto1 = - (target1 - outo1)
  36.         pdOuto1Neto1 = sigmoidDerivationx(outo1)
  37.         pdNeto1W5 = outh1
  38.         pdEW5 = pdEOuto1 * pdOuto1Neto1 * pdNeto1W5
  39.         pdNeto1W6 = outh2
  40.         pdEW6 = pdEOuto1 * pdOuto1Neto1 * pdNeto1W6
  41.         pdEOuto2 = - (target2 - outo2)
  42.         pdOuto2Neto2 = sigmoidDerivationx(outo2)
  43.         pdNeto1W7 = outh1
  44.         pdEW7 = pdEOuto2 * pdOuto2Neto2 * pdNeto1W7
  45.         pdNeto1W8 = outh2
  46.         pdEW8 = pdEOuto2 * pdOuto2Neto2 * pdNeto1W8
  47.         # 计算w1-w4(输出层权重)的误差
  48.         pdEOuto1 = - (target1 - outo1) #之前算过
  49.         pdEOuto2 = - (target2 - outo2)  #之前算过
  50.         pdOuto1Neto1 = sigmoidDerivationx(outo1)    #之前算过
  51.         pdOuto2Neto2 = sigmoidDerivationx(outo2)    #之前算过
  52.         pdNeto1Outh1 = weight[5-1]
  53.         pdNeto1Outh2 = weight[7-1]
  54.         pdENeth1 = pdEOuto1 * pdOuto1Neto1 * pdNeto1Outh1 + pdEOuto2 * pdOuto2Neto2 * pdNeto1Outh2
  55.         pdOuth1Neth1 = sigmoidDerivationx(outh1)
  56.         pdNeth1W1 = i1
  57.         pdNeth1W2 = i2
  58.         pdEW1 = pdENeth1 * pdOuth1Neth1 * pdNeth1W1
  59.         pdEW2 = pdENeth1 * pdOuth1Neth1 * pdNeth1W2
  60.         pdNeto1Outh2 = weight[6-1]
  61.         pdNeto2Outh2 = weight[8-1]
  62.         pdOuth2Neth2 = sigmoidDerivationx(outh2)
  63.         pdNeth1W3 = i1
  64.         pdNeth1W4 = i2
  65.         pdENeth2 = pdEOuto1 * pdOuto1Neto1 * pdNeto1Outh2 + pdEOuto2 * pdOuto2Neto2 * pdNeto2Outh2
  66.         pdEW3 = pdENeth2 * pdOuth2Neth2 * pdNeth1W3
  67.         pdEW4 = pdENeth2 * pdOuth2Neth2 * pdNeth1W4
  68.         #权重更新
  69.         weight[1-1] = weight[1-1] - alpha * pdEW1
  70.         weight[2-1] = weight[2-1] - alpha * pdEW2
  71.         weight[3-1] = weight[3-1] - alpha * pdEW3
  72.         weight[4-1] = weight[4-1] - alpha * pdEW4
  73.         weight[5-1] = weight[5-1] - alpha * pdEW5
  74.         weight[6-1] = weight[6-1] - alpha * pdEW6
  75.         weight[7-1] = weight[7-1] - alpha * pdEW7
  76.         weight[8-1] = weight[8-1] - alpha * pdEW8
  77.         # print(weight[1-1])
  78.         # print(weight[2-1])
  79.         # print(weight[3-1])
  80.         # print(weight[4-1])
  81.         # print(weight[5-1])
  82.         # print(weight[6-1])
  83.         # print(weight[7-1])
  84.         # print(weight[8-1])

  不知道你是否对此感到熟悉一点了呢？反正我按照公式实现一遍之后深有体会，然后用向量的又写了一次代码。
  接下来我们要用向量来存储这些权重，输出结果等，因为如果我们不这样做，你看上面的例子就知道我们需要写很多w1,w2等，这要是参数一多就很可怕。
  这些格式我是参考吴恩达的格式，相关课程资料->吴恩达深度学习视频。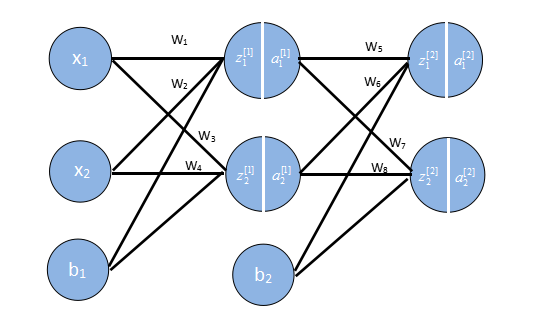
神经网络
我将原文的图片的变量名改成如上
然后正向传播的公式如下：

z[1]1=w[1]1T⋅x+b1,a[1]1=σ(z[1]1)z[1]2=w[1]2T⋅x+b1,a[1]2=σ(z[1]2)z[2]1=w[2]1T⋅a1+b2,a[2]1=σ(z[2]1)z[2]2=w[2]2T⋅a1+b2,a[2]2=σ(z[2]2)(9)(10)(11)(12)(13) (9) z 1 [ 1 ] = w 1 [ 1 ] T ⋅ x + b 1 , a 1 [ 1 ] = σ ( z 1 [ 1 ] ) (10) z 2 [ 1 ] = w 2 [ 1 ] T ⋅ x + b 1 , a 2 [ 1 ] = σ ( z 2 [ 1 ] ) (11) z 1 [ 2 ] = w 1 [ 2 ] T ⋅ a 1 + b 2 , a 1 [ 2 ] = σ ( z 1 [ 2 ] ) (12) z 2 [ 2 ] = w 2 [ 2 ] T ⋅ a 1 + b 2 , a 2 [ 2 ] = σ ( z 2 [ 2 ] ) (13)

其中

w[1]1T=(w1,w2)w[1]2T=(w3,w4)w[2]1T=(w5,w6)w[2]2T=(w7,w8)(14)(15)(16)(17) (14) w 1 [ 1 ] T = ( w 1 , w 2 ) (15) w 2 [ 1 ] T = ( w 3 , w 4 ) (16) w 1 [ 2 ] T = ( w 5 , w 6 ) (17) w 2 [ 2 ] T = ( w 7 , w 8 )

然后反向传播的公式如下：

∂E∂w[2]1=∂E∂a[2]1⋅∂a[2]1∂z[2]1⋅∂z[2]1∂w[2]1∂E∂w[2]1=∂E∂a[2]2⋅∂a[2]2∂z[2]2⋅∂z[2]2∂w[2]2∂E∂w[1]1=∂E∂a[1]1⋅∂a[1]1∂z[1]1⋅∂z[1]1∂w[1]1∂E∂w[1]2=∂E∂a[1]2⋅∂a[1]2∂z[1]2⋅∂z[1]2∂w[1]2(18)(19)(20)(21) (18) ∂ E ∂ w 1 [ 2 ] = ∂ E ∂ a 1 [ 2 ] ⋅ ∂ a 1 [ 2 ] ∂ z 1 [ 2 ] ⋅ ∂ z 1 [ 2 ] ∂ w 1 [ 2 ] (19) ∂ E ∂ w 1 [ 2 ] = ∂ E ∂ a 2 [ 2 ] ⋅ ∂ a 2 [ 2 ] ∂ z 2 [ 2 ] ⋅ ∂ z 2 [ 2 ] ∂ w 2 [ 2 ] (20) ∂ E ∂ w 1 [ 1 ] = ∂ E ∂ a 1 [ 1 ] ⋅ ∂ a 1 [ 1 ] ∂ z 1 [ 1 ] ⋅ ∂ z 1 [ 1 ] ∂ w 1 [ 1 ] (21) ∂ E ∂ w 2 [ 1 ] = ∂ E ∂ a 2 [ 1 ] ⋅ ∂ a 2 [ 1 ] ∂ z 2 [ 1 ] ⋅ ∂ z 2 [ 1 ] ∂ w 2 [ 1 ]

具体地

∂E∂a[2]1=−(y1−a[2]1)∂a[2]1∂z[2]1=a[2]1(1−a[2]1)∂z[2]1∂w[2]1=a[2]1∂E∂a[2]2=−(y2−a[2]2)∂a[2]1∂z[2]1=a[2]2(1−a[2]2)∂z[2]1∂w[2]2=a[2]2∂E∂a[1]1=w[2]1Tδ2∂a[1]1∂z[1]1=a[1]1⋅(1−a[1]1)∂z[1]1∂w[1]1=a[1]1∂E∂a[1]1=w[2]2Tδ2∂a[1]2∂z[1]1=a[1]2⋅(1−a[1]2)∂z[1]1∂w[1]2=a[1]2(22)(23)(24)(25)(26)(27)(28)(29)(30)(31)(32)(33) (22) ∂ E ∂ a 1 [ 2 ] = − ( y 1 − a 1 [ 2 ] ) (23) ∂ a 1 [ 2 ] ∂ z 1 [ 2 ] = a 1 [ 2 ] ( 1 − a 1 [ 2 ] ) (24) ∂ z 1 [ 2 ] ∂ w 1 [ 2 ] = a 1 [ 2 ] (25) ∂ E ∂ a 2 [ 2 ] = − ( y 2 − a 2 [ 2 ] ) (26) ∂ a 1 [ 2 ] ∂ z 1 [ 2 ] = a 2 [ 2 ] ( 1 − a 2 [ 2 ] ) (27) ∂ z 1 [ 2 ] ∂ w 2 [ 2 ] = a 2 [ 2 ] (28) ∂ E ∂ a 1 [ 1 ] = w 1 [ 2 ] T δ 2 (29) ∂ a 1 [ 1 ] ∂ z 1 [ 1 ] = a 1 [ 1 ] ⋅ ( 1 − a 1 [ 1 ] ) (30) ∂ z 1 [ 1 ] ∂ w 1 [ 1 ] = a 1 [ 1 ] (31) ∂ E ∂ a 1 [ 1 ] = w 2 [ 2 ] T δ 2 (32) ∂ a 2 [ 1 ] ∂ z 1 [ 1 ] = a 2 [ 1 ] ⋅ ( 1 − a 2 [ 1 ] ) (33) ∂ z 1 [ 1 ] ∂ w 2 [ 1 ] = a 2 [ 1 ]

其中

δ2=⎛⎝⎜⎜⎜⎜⎜⎜∂E∂a[2]1⋅∂a[2]1∂z[2]1∂E∂a[2]2⋅∂a[2]2∂z[2]2(34)(35)⎞⎠⎟⎟⎟⎟⎟⎟=(∂E∂a[2]⋅∂a[2]∂z[2]) δ 2 = ( (34) ∂ E ∂ a 1 [ 2 ] ⋅ ∂ a 1 [ 2 ] ∂ z 1 [ 2 ] (35) ∂ E ∂ a 2 [ 2 ] ⋅ ∂ a 2 [ 2 ] ∂ z 2 [ 2 ] ) = ( ∂ E ∂ a [ 2 ] ⋅ ∂ a [ 2 ] ∂ z [ 2 ] )

为啥这样写呢，一开始我也没明白，后来看到 ∂E∂a[2]1⋅∂a[2]1∂z[2]1 ∂ E ∂ a 1 [ 2 ] ⋅ ∂ a 1 [ 2 ] ∂ z 1 [ 2 ] 有好几次重复，且也便于梯度公式的书写。

  1. import numpy as np
  3. def sigmoid(x):
  4.     return 1 / (1 + np.exp(-x))
  5. def sigmoidDerivationx(y):
  6.     return y * (1 - y)
  8. if __name__ == '__main__':
  9.     #初始化一些参数
  10.     alpha = 0.5
  11.     w1 = [[0.15, 0.20], [0.25, 0.30]] #Weight of input layer
  12.     w2 = [[0.40, 0.45], [0.50, 0.55]]
  13.     b1 = 0.35
  14.     b2 = 0.60
  15.     x = [0.05, 0.10]
  16.     y = [0.01, 0.99]
  17.     #前向传播
  18.     z1 = np.dot(w1, x) + b1
  19.     a1 = sigmoid(z1)
  20.     z2 = np.dot(w2, a1) + b2
  21.     a2 = sigmoid(z2)
  22.     for n in range(10000):
  23.         #反向传播 使用代价函数为C=1 / (2n) * sum[(y-a2)^2]
  24.         #分为两次
  25.         # 一次是最后一层对前面一层的错误
  26.         delta2 = np.multiply(-(y-a2), np.multiply(a2, 1-a2))
  27.         # for i in range(len(w2)):
  28.         #     print(w2[i] - alpha * delta2[i] * a1)
  29.         #计算非最后一层的错误
  30.         # print(delta2)
  31.         delta1 = np.multiply(np.dot(w1, delta2), np.multiply(a1, 1-a1))
  32.         # print(delta1)
  33.         # for i in range(len(w1)):
  34.             # print(w1[i] - alpha * delta1[i] * np.array(x))
  35.         #更新权重
  36.         for i in range(len(w2)):
  37.             w2[i] = w2[i] - alpha * delta2[i] * a1
  38.         for i in range(len(w1)):
  39.             w1[i] - alpha * delta1[i] * np.array(x)
  40.         #继续前向传播，算出误差值
  41.         z1 = np.dot(w1, x) + b1
  42.         a1 = sigmoid(z1)
  43.         z2 = np.dot(w2, a1) + b2
  44.         a2 = sigmoid(z2)
  45.         print(str(n) + " result:" + str(a2[0]) + ", result:" +str(a2[1]))
  46.         # print(str(n) + "  error1:" + str(y[0] - a2[0]) + ", error2:" +str(y[1] - a2[1]))

可以看到，用向量来表示的话代码就简短了非常多。但是用了向量化等的方法，如果不太熟，去看吴恩达深度学习的第一部分，再返过来看就能懂了。
下面，来看一个例子。用神经网络实现XOR（01=1，10=1，00=0，11=0）。我们都知道感知机是没法实现异或的，原因是线性不可分。
接下里的这个例子，我是用2个输入结点，3个隐层结点，1个输出结点来实现的。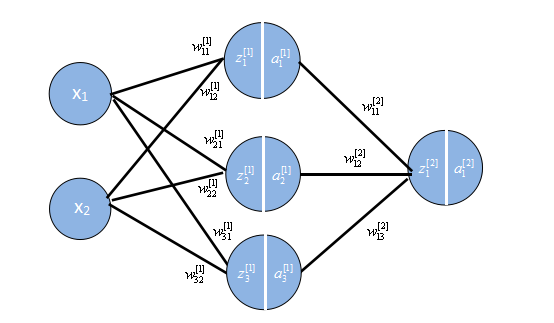
异或
让我们以一个输入为例。
前向传播：

⎛⎝⎜⎜⎜w[1]11w[1]12w[1]21w[1]22w[1]31w[1]32⎞⎠⎟⎟⎟⋅(x1x2)=⎛⎝⎜⎜⎜z[1]1z[1]2z[1]3⎞⎠⎟⎟⎟ ( w 11 [ 1 ] w 12 [ 1 ] w 21 [ 1 ] w 22 [ 1 ] w 31 [ 1 ] w 32 [ 1 ] ) ⋅ ( x 1 x 2 ) = ( z 1 [ 1 ] z 2 [ 1 ] z 3 [ 1 ] )

⎛⎝⎜⎜⎜a[1]1a[1]2a[1]3⎞⎠⎟⎟⎟=⎛⎝⎜⎜⎜σ(z[1]1)σ(z[1]2)σ(z[1]3)⎞⎠⎟⎟⎟ ( a 1 [ 1 ] a 2 [ 1 ] a 3 [ 1 ] ) = ( σ ( z 1 [ 1 ] ) σ ( z 2 [ 1 ] ) σ ( z 3 [ 1 ] ) )

(w[2]11w[2]12w[2]13)⎛⎝⎜⎜⎜a[1]1a[1]2a[1]3⎞⎠⎟⎟⎟=(z[2]1) ( w 11 [ 2 ] w 12 [ 2 ] w 13 [ 2 ] ) ( a 1 [ 1 ] a 2 [ 1 ] a 3 [ 1 ] ) = ( z 1 [ 2 ] )

(a[2]1)=(σ(z[2]1)) ( a 1 [ 2 ] ) = ( σ ( z 1 [ 2 ] ) )

反向传播：
主要是有2个公式比较重要

δL=∇aC⊙σ′(aL)=−(y−aL)⊙(aL(1−aL)) δ L = ∇ a C ⊙ σ ′ ( a L ) = − ( y − a L ) ⊙ ( a L ( 1 − a L ) )

原理同上

δl=((wl+1)T)⊙σ′(al) δ l = ( ( w l + 1 ) T ) ⊙ σ ′ ( a l )

wl=wl−ηδl(al−1)T w l = w l − η δ l ( a l − 1 ) T

这次省略了偏导，代码如下

  1. import numpy as np
  2. # sigmoid function
  3. def sigmoid(x):
  4.     return 1 / (1 + np.exp(-x))
  5. def sigmoidDerivationx(y):
  6.     return y * (1 - y)
  8. if __name__ == '__main__':
  9.     alpha = 1
  10.     input_dim = 2
  11.     hidden_dim = 3
  12.     output_dim = 1
  13.     synapse_0 = 2 * np.random.random((hidden_dim, input_dim)) - 1  #(2, 3)
  14.     # synapse_0 = np.ones((hidden_dim, input_dim)) * 0.5
  15.     synapse_1 = 2 * np.random.random((output_dim, hidden_dim)) - 1  #(2, 2)
  16.     # synapse_1 = np.ones((output_dim, hidden_dim)) * 0.5
  17.     x = np.array([[0, 1], [1, 0], [0, 0], [1, 1]]).T #(2, 4)
  18.     # x = np.array([[0, 1]]).T #(3, 1)
  19.     y = np.array([[1], [1], [0], [0]]).T    #(1, 4)
  20.     # y = np.array([[1]]).T    #(2, 1)
  21.     for i in range(2000000):
  22.         z1 = np.dot(synapse_0, x)   #(3, 4)
  23.         a1 = sigmoid(z1)    #(3, 4)
  24.         z2 = np.dot(synapse_1, a1)  #(1, 4)
  25.         a2 = sigmoid(z2)    #(1, 4)
  26.         error = -(y - a2) #(1, 4)
  27.         delta2 = np.multiply(-(y - a2) / x.shape[1], sigmoidDerivationx(a2))  #(1, 4)
  28.         delta1 = np.multiply(np.dot(synapse_1.T, delta2), sigmoidDerivationx(a1))  #(3, 4)
  29.         synapse_1 = synapse_1 - alpha * np.dot(delta2, a1.T) #(1, 3)
  30.         synapse_0 = synapse_0 - alpha * np.dot(delta1, x.T) #(3, 2)
  31.         print(str(i) + ":", end=' ')
  32.         print(a2)

发表评论

表情：
评论列表 （有 0 条评论，287人围观）

还没有评论，来说两句吧...

相关阅读