BP反向传播详细推导

￡神魔★判官ぃ 2021-11-11 06:50 475阅读 0赞

BP神经网络是反向传播算法，他是一个非线性的前馈神经网络。由于网络参数需要更新，反向指的是参数梯度的反向传播，输入向前传播。非线性是因为神经元的激活函数是一个非线性可导的sigmoid函数。先来看看神经元的激活函数，即sigmoid函数：

![\{\\rm\{f(x) = sigmoid\}\}(x) = \\frac\{1\}\{\{1 + \{e^\{ - x\}\}\}\}][rm_f_x_ _ sigmoid_x_ _ _frac_1_1 _ _e_ - x]

该函数的特点是：

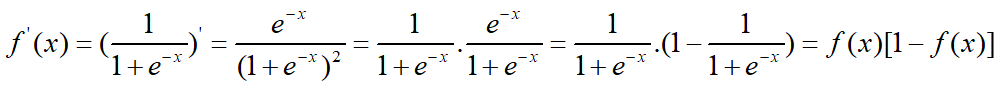
![20190804171047909.png][]

其图像为：

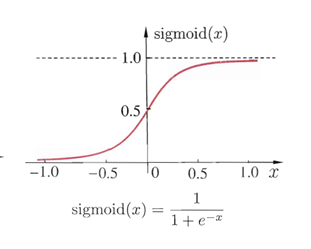
![watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MDY3MTQyNQ_size_16_color_FFFFFF_t_70][]

Sigmoid函数把可能在较大范围内变化的输入值挤压到（0，1）的范围内，并且该函数是可导的。当然，sigmoid函数只是神经元激活函数的一种，但却是最常用的一种激活函数。

首先，我们来看看BP算法的真面目。给定一个训练集（含有m个样本）。

![D = \\\{ (\{x\_1\},\{y\_x\}),(\{x\_2\},\{y\_2\}),...,(\{x\_m\},\{y\_m\})\\\}][D _ _ _x_1_y_x_x_2_y_2_..._x_m_y_m]，其中![\{x\_i\} \\in \{\{\\rm\{R\}\}^d\}][x_i_ _in _rm_R_d]表示输入由 d 个属性描述（特征维度为d），![\{y\_i\} \\in \{R^l\}][y_i_ _in _R_l]表示输出为 ![l][] 维实值向量（l 个类别）。为了便于讨论，下图给出了一个拥有 ![d][] 个输入神经元，![l][] 个输出神经元和 ![q][] 个隐藏神经元的多层前馈神经网络。该网络包含一个输出层，一个隐藏层，一个输出层。其中隐藏层的阈值是 ![\\gamma][gamma] ，输出层的阈值是 ![\\theta][theta]。

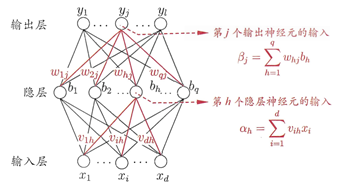
![20190804171807174.png][]

现在设定符号标准：

![\{\\nu \_\{ih\}\}][nu _ih]：输入层第i个神经元和隐藏层第h个神经元之间连接的权值

![\{\\omega \_\{hj\}\}][omega _hj]：隐藏层第h个神经元和输出层第j个神经元之间连接的权值

![\{\\alpha \_h\} = \\sum\\limits\_\{i = 1\}^d \{\{\\nu \_\{ih\}\}\{x\_\{\\rm\{i\}\}\}\}][alpha _h_ _ _sum_limits_i _ 1_d _nu _ih_x_rm_i]：隐藏层第h个神经元的输入，![\{x\_\{\\rm\{i\}\}\}][x_rm_i] 是输入层的第i个输入

![\{\\beta \_j\} = \\sum\\limits\_\{h = 1\}^\{\\rm\{q\}\} \{\{\\omega \_\{hj\}\}\{b\_h\}\}][beta _j_ _ _sum_limits_h _ 1_rm_q_ _omega _hj_b_h]：输出层第j个神经元的输入，![\{b\_h\}][b_h] 是输出层的输入，也就是隐藏层的输出

![\{b\_h\} = f(\{\\alpha \_h\} - \{\\gamma \_h\})][b_h_ _ f_alpha _h_ - _gamma _h]：隐藏层第h个神经元的输出，即输出层的第h个输入，![\{\\gamma \_h\}][gamma _h] 是隐藏层第h个神经元的阈值（偏置）

![\\mathop \{y\_j^k\}\\limits^\\^ = f(\{\\beta \_j\} - \{\\theta \_j\})][mathop _y_j_k_limits_ _ f_beta _j_ - _theta _j]：第k个输入神经元的网络输出![\\mathop \{\{y\_k\}\}\\limits^\\^ = (\\mathop \{y\_1^k\}\\limits^\\^ ,\\mathop \{y\_2^k\}\\limits^\\^ ,...,\\mathop \{y\_l^k\}\\limits^\\^ )][mathop _y_k_limits_ _ _mathop _y_1_k_limits_ _mathop _y_2_k_limits_ _..._mathop _y_l_k_limits_]，![\{\\theta \_j\}][theta _j]是输出层的阈值（偏置）

![\{y\_j\}][y_j]：输出层第j个神经元的理想输出

根据神经网路结构图可以看出网络中要确定的变量个数是 ![(d + l + 1)q + l][d _ l _ 1_q _ l] 个，其中输入层到隐藏层有d\*q个权值变量，隐藏层到输出层有![q\*l][q_l]个权值变量，还包括q个隐藏层神经元阈值和 l 个输出层神经元阈值。

则网络在![(\{x\_k\},\{y\_k\})][x_k_y_k]上的均方误差为：![\{E\_k\} = \\frac\{1\}\{2\}\\sum\\limits\_\{j = 1\}^l \{\{\{(\\mathop \{y\_j^k\}\\limits^\\^ - y\_j^k)\}^2\}\}][E_k_ _ _frac_1_2_sum_limits_j _ 1_l _mathop _y_j_k_limits_ - y_j_k_2]

BP神经网络的思想是根据均方误差，来调整每条连接线的权值和阈值(偏置)。从而使均方误差达到一个可以接受的值。

阈值是用来衡量是否可以结束神经网络算法的一个条件（当然还有其他的结束条件，达到一定的迭代次数，误差降低到某一程度。）

下面进行神经网络算法的推倒过程：（采用随机梯度下降法）

第k个输出样本在输出层的均方误差为：![\{E\_k\} = \\frac\{1\}\{2\}\\sum\\limits\_\{j = 1\}^l \{\{\{(\\mathop \{y\_j^k\}\\limits^\\^ - y\_j^k)\}^2\}\}][E_k_ _ _frac_1_2_sum_limits_j _ 1_l _mathop _y_j_k_limits_ - y_j_k_2]

现在以隐藏层到输出层的权值和阈值（偏置）调整方案为例：

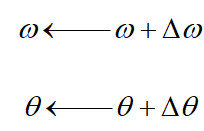
![20190804172728361.png][]

定义：![\\Delta \{\\omega \_\{hj\}\} = - \\eta \\frac\{\{\\partial \{E\_k\}\}\}\{\{\\partial \{\\omega \_\{hj\}\}\}\}][Delta _omega _hj_ _ - _eta _frac_partial _E_k_partial _omega _hj] ，即用梯度下降法来调整权值的变化，其中负号表示梯度下降的方向，![\\eta][eta]表示学习效率（或叫做调整步长），一般取（0,1）。

因为： ![\{\\omega \_\{hj\}\}][omega _hj]对输出层的输入![\{\\beta \_\{\\rm\{j\}\}\}][beta _rm_j]和输出层的输出![\\mathop \{y\_j^k\}\\limits^\\^][mathop _y_j_k_limits]都有影响，

所以：![\\frac\{\{\\partial \{E\_k\}\}\}\{\{\\partial \{\\omega \_\{hj\}\}\}\} = \\frac\{\{\\partial \{E\_k\}\}\}\{\{\\partial \\mathop \{y\_j^k\}\\limits^\\^ \}\}.\\frac\{\{\\partial \\mathop \{\{\\rm\{y\}\}\_j^k\}\\limits^\\^ \}\}\{\{\\partial \{\\beta \_j\}\}\}.\\frac\{\{\\partial \{\\beta \_j\}\}\}\{\{\\partial \{\\omega \_\{hj\}\}\}\}][frac_partial _E_k_partial _omega _hj_ _ _frac_partial _E_k_partial _mathop _y_j_k_limits_ _._frac_partial _mathop _rm_y_j_k_limits_ _partial _beta _j_._frac_partial _beta _j_partial _omega _hj]

而 ![\\frac\{\{\\partial \{\\beta \_j\}\}\}\{\{\\partial \{\\omega \_\{hj\}\}\}\} = \{b\_h\}][frac_partial _beta _j_partial _omega _hj_ _ _b_h]，![\\frac\{\{\\partial \\mathop \{\{\\rm\{y\}\}\_j^k\}\\limits^\\^ \}\}\{\{\\partial \{\\beta \_j\}\}\} = \\mathop \{\{\\rm\{y\}\}\_j^k\}\\limits^\\^ (1 - \\mathop \{\{\\rm\{y\}\}\_j^k\}\\limits^\\^ )][frac_partial _mathop _rm_y_j_k_limits_ _partial _beta _j_ _ _mathop _rm_y_j_k_limits_ _1 - _mathop _rm_y_j_k_limits_]。因为![\{\\beta \_j\}][beta _j]是经过输出层神经元激活函数后得到输出![\\mathop \{\{\\rm\{y\}\}\_j^k\}\\limits^\\^][mathop _rm_y_j_k_limits]

![\\frac\{\{\\partial \{E\_k\}\}\}\{\{\\partial \\mathop \{y\_j^k\}\\limits^\\^ \}\} = \\frac\{\{\\partial (\\frac\{1\}\{2\}\\sum\\limits\_\{j = 1\}^l \{\{\{(\\mathop \{y\_j^k\}\\limits^\\^ - y\_j^k)\}^2\}\} )\}\}\{\{\\partial \\mathop \{y\_j^k\}\\limits^\\^ \}\} = (\\mathop \{y\_j^k\}\\limits^\\^ - y\_j^k)][frac_partial _E_k_partial _mathop _y_j_k_limits_ _ _ _frac_partial _frac_1_2_sum_limits_j _ 1_l _mathop _y_j_k_limits_ - y_j_k_2_ _partial _mathop _y_j_k_limits_ _ _ _mathop _y_j_k_limits_ - y_j_k]带入上述公式得

![\\frac\{\{\\partial \{E\_k\}\}\}\{\{\\partial \{\\omega \_\{hj\}\}\}\} = (\\mathop \{y\_j^k\}\\limits^\\^ - y\_j^k)\\mathop \{\{\\rm\{y\}\}\_j^k\}\\limits^\\^ (1 - \\mathop \{\{\\rm\{y\}\}\_j^k\}\\limits^\\^ )\{b\_b\}][frac_partial _E_k_partial _omega _hj_ _ _mathop _y_j_k_limits_ - y_j_k_mathop _rm_y_j_k_limits_ _1 - _mathop _rm_y_j_k_limits_ _b_b]

令：![\{g\_j\} = - \\frac\{\{\\partial \{E\_k\}\}\}\{\{\\partial \\mathop \{y\_j^k\}\\limits^\\^ \}\}.\\frac\{\{\\partial \\mathop \{\{\\rm\{y\}\}\_j^k\}\\limits^\\^ \}\}\{\{\\partial \{\\beta \_j\}\}\} = - (\\mathop \{y\_j^k\}\\limits^\\^ - y\_j^k)\\mathop \{\{\\rm\{y\}\}\_j^k\}\\limits^\\^ (1 - \\mathop \{\{\\rm\{y\}\}\_j^k\}\\limits^\\^ )][g_j_ _ - _frac_partial _E_k_partial _mathop _y_j_k_limits_ _._frac_partial _mathop _rm_y_j_k_limits_ _partial _beta _j_ _ - _mathop _y_j_k_limits_ - y_j_k_mathop _rm_y_j_k_limits_ _1 - _mathop _rm_y_j_k_limits_]

则： ![\\Delta \\omega = \\frac\{\{\\partial \{E\_k\}\}\}\{\{\\partial \{\\omega \_\{hj\}\}\}\} = \\eta \{g\_j\}\{b\_n\}][Delta _omega _ _frac_partial _E_k_partial _omega _hj_ _ _eta _g_j_b_n] ——》这是 ![\\omega][omega] 的调整方法：

现在推倒 ![\\theta][theta] 的调整方法：

![\\Delta \{\\theta \_j\} = - \\eta \\frac\{\{\\partial \{E\_\{\\rm\{k\}\}\}\}\}\{\{\\partial \{\\theta \_j\}\}\} = - \\eta \\frac\{\{\\partial (\\frac\{1\}\{2\}\\sum\\limits\_\{j = 1\}^l \{\{\{(\\mathop \{y\_j^k\}\\limits^\\^ - y\_j^k)\}^2\}\} )\}\}\{\{\\partial \{\\theta \_j\}\}\} = - \\eta \\frac\{\{(\\mathop \{y\_j^k\}\\limits^\\^ - y\_j^k)\\partial f(\{\\beta \_l\} - \{\\theta \_j\})\}\}\{\{\\partial \{\\theta \_j\}\}\} = - \\eta ( - \\mathop \{y\_j^k\}\\limits^\\^ (\\mathop \{y\_j^k\}\\limits^\\^ - y\_j^k)(1 - \\mathop \{y\_j^k\}\\limits^\\^ )) = - \\eta \{g\_j\}][Delta _theta _j_ _ - _eta _frac_partial _E_rm_k_partial _theta _j_ _ - _eta _frac_partial _frac_1_2_sum_limits_j _ 1_l _mathop _y_j_k_limits_ - y_j_k_2_ _partial _theta _j_ _ - _eta _frac_mathop _y_j_k_limits_ - y_j_k_partial f_beta _l_ - _theta _j_partial _theta _j_ _ - _eta _ - _mathop _y_j_k_limits_ _mathop _y_j_k_limits_ - y_j_k_1 - _mathop _y_j_k_limits_ _ _ - _eta _g_j]

到此，权重和阈值的调整方法都已经知道了:

现在我们再来推倒一下![\\Delta \{\\nu \_\{ih\}\}][Delta _nu _ih]，因为![\\Delta \{\\nu \_\{ih\}\}][Delta _nu _ih]的影响路径：![\\Delta \{\\nu \_\{ih\}\} \\to \{\\alpha \_h\} \\to \{b\_h\}][Delta _nu _ih_ _to _alpha _h_ _to _b_h]

![\\Delta \{\\nu \_\{ih\}\} = - \\eta \\frac\{\{\\partial \{E\_k\}\}\}\{\{\\partial \{\\nu \_\{ih\}\}\}\} = - \\eta \\frac\{\{\\partial \{E\_k\}\}\}\{\{\\partial \{b\_h\}\}\}.\\frac\{\{\\partial \{b\_h\}\}\}\{\{\\partial \{\\alpha \_h\}\}\}.\\frac\{\{\\partial \{\\alpha \_h\}\}\}\{\{\\partial \{\\nu \_\{ih\}\}\}\}][Delta _nu _ih_ _ - _eta _frac_partial _E_k_partial _nu _ih_ _ - _eta _frac_partial _E_k_partial _b_h_._frac_partial _b_h_partial _alpha _h_._frac_partial _alpha _h_partial _nu _ih]

其中：![\\frac\{\{\\partial \{\\alpha \_h\}\}\}\{\{\\partial \{\\nu \_\{ih\}\}\}\} = \{x\_i\}][frac_partial _alpha _h_partial _nu _ih_ _ _x_i]

令：

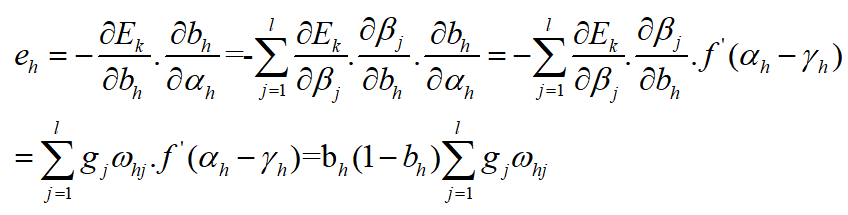
![watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MDY3MTQyNQ_size_16_color_FFFFFF_t_70 1][]

注意第二个等号的理解：即第k个样本在输出层的误差是输出层的 ![l][] 神经元的误差和，那么 ![\{b\_h\}][b_h]， 是隐藏层的第h个输出，即输出层的第h个输入（还没乘以权值），这个输入对输出层的每一个神经元都有影响，所以有一个求和的过程。

所以：![\\Delta \{\\nu \_\{ih\}\} = \\eta \{e\_h\}\{x\_i\}][Delta _nu _ih_ _ _eta _e_h_x_i]

同理可得：![\\Delta \\gamma = - \\eta \{e\_h\}][Delta _gamma _ - _eta _e_h]

所谓误差的反向传播（我的理解）：根据公式即可发现，每一层权值和偏置的调整，都跟其直接相连接的下一次输出值的误差有关。即，输出的结果，对于权值和偏置的调整是有影响的。这也是，BP模型权值和偏置调整公式的定义。

现在的几个问题：

1，梯度的几何意义？

2，![\\Delta \\omega][Delta _omega]的变化，是正数？是负数？正数代表的含义？负数代表的含义？

3，随机梯度下降和标准梯度下降？

4，解决过拟合问题？

5， ![\\eta][eta] 的大小怎么定？

问题1：

![20190804174710258.png][]

函数在某一点的梯度，垂直于该点的等值面，指向函数增大的方向。

问题2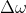：![\\Delta \\omega][Delta _omega 1]就是梯度乘上一个因子

问题3：标准梯度下降和随机梯度下降的关键区别是：

(1) 标准梯度下降是在权值更新前对所有样本汇总误差，而随机梯度下降的权值是通过考察每一个训练样本实例来更新。

(2) 标准梯度下降因为要对所有样本汇总误差，计算量更大。这样，每一次权值更新比随机梯度下降所用的步长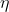（![\\eta][eta 1]）更大

(3) 如果误差![E(\\omega )][E_omega]有多个极小值，随机梯度下降可能避免陷入这些局部极小值。因为采用不同的![\\Delta \{E\_k\}(\\omega )][Delta _E_k_omega]而不是![\\Delta E(\\omega )][Delta E_omega]

(4) 使用随机梯度下降，可以最小化均方误差。

问题4：迭代次数太少，误差过大，发生欠拟合。迭代次数过多，在训练样本上，误差很小。出现过拟合。权值衰减法。为算法提供一套验证数据集。

问题5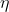：![\\eta][eta 1] 一般被设定为一个很小的数值，有时候会使其随着权调整次数的增加而衰减。（放慢学习速率，减小步长）。因为在迭代一定次数过后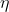，![\\eta][eta 1]过大，可能会使梯度下降跳过全局最小值。

[rm_f_x_ _ sigmoid_x_ _ _frac_1_1 _ _e_ - x]: https://private.codecogs.com/gif.latex?%7B%5Crm%7Bf%28x%29%20%3D%20sigmoid%7D%7D%28x%29%20%3D%20%5Cfrac%7B1%7D%7B%7B1%20&plus;%20%7Be%5E%7B%20-%20x%7D%7D%7D%7D
[20190804171047909.png]: /images/20211109/b64d700d500f425db5fb44dfe6009958.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MDY3MTQyNQ_size_16_color_FFFFFF_t_70]: /images/20211109/33f68c8f70a342b59dade141a214c52d.png
[D _ _ _x_1_y_x_x_2_y_2_..._x_m_y_m]: https://private.codecogs.com/gif.latex?D%20%3D%20%5C%7B%20%28%7Bx_1%7D%2C%7By_x%7D%29%2C%28%7Bx_2%7D%2C%7By_2%7D%29%2C...%2C%28%7Bx_m%7D%2C%7By_m%7D%29%5C%7D
[x_i_ _in _rm_R_d]: https://private.codecogs.com/gif.latex?%7Bx_i%7D%20%5Cin%20%7B%7B%5Crm%7BR%7D%7D%5Ed%7D
[y_i_ _in _R_l]: https://private.codecogs.com/gif.latex?%7By_i%7D%20%5Cin%20%7BR%5El%7D
[l]: https://private.codecogs.com/gif.latex?l
[d]: https://private.codecogs.com/gif.latex?d
[q]: https://private.codecogs.com/gif.latex?q
[gamma]: https://private.codecogs.com/gif.latex?%5Cgamma
[theta]: https://private.codecogs.com/gif.latex?%5Ctheta
[20190804171807174.png]: /images/20211109/500bb4410710493999f906f597a9645a.png
[nu _ih]: https://private.codecogs.com/gif.latex?%7B%5Cnu%20_%7Bih%7D%7D
[omega _hj]: https://private.codecogs.com/gif.latex?%7B%5Comega%20_%7Bhj%7D%7D
[alpha _h_ _ _sum_limits_i _ 1_d _nu _ih_x_rm_i]: https://private.codecogs.com/gif.latex?%7B%5Calpha%20_h%7D%20%3D%20%5Csum%5Climits_%7Bi%20%3D%201%7D%5Ed%20%7B%7B%5Cnu%20_%7Bih%7D%7D%7Bx_%7B%5Crm%7Bi%7D%7D%7D%7D
[x_rm_i]: https://private.codecogs.com/gif.latex?%7Bx_%7B%5Crm%7Bi%7D%7D%7D
[beta _j_ _ _sum_limits_h _ 1_rm_q_ _omega _hj_b_h]: https://private.codecogs.com/gif.latex?%7B%5Cbeta%20_j%7D%20%3D%20%5Csum%5Climits_%7Bh%20%3D%201%7D%5E%7B%5Crm%7Bq%7D%7D%20%7B%7B%5Comega%20_%7Bhj%7D%7D%7Bb_h%7D%7D
[b_h]: https://private.codecogs.com/gif.latex?%7Bb_h%7D
[b_h_ _ f_alpha _h_ - _gamma _h]: https://private.codecogs.com/gif.latex?%7Bb_h%7D%20%3D%20f%28%7B%5Calpha%20_h%7D%20-%20%7B%5Cgamma%20_h%7D%29
[gamma _h]: https://private.codecogs.com/gif.latex?%7B%5Cgamma%20_h%7D
[mathop _y_j_k_limits_ _ f_beta _j_ - _theta _j]: https://private.codecogs.com/gif.latex?%5Cmathop%20%7By_j%5Ek%7D%5Climits%5E%5C%5E%20%3D%20f%28%7B%5Cbeta%20_j%7D%20-%20%7B%5Ctheta%20_j%7D%29
[mathop _y_k_limits_ _ _mathop _y_1_k_limits_ _mathop _y_2_k_limits_ _..._mathop _y_l_k_limits_]: https://private.codecogs.com/gif.latex?%5Cmathop%20%7B%7By_k%7D%7D%5Climits%5E%5C%5E%20%3D%20%28%5Cmathop%20%7By_1%5Ek%7D%5Climits%5E%5C%5E%20%2C%5Cmathop%20%7By_2%5Ek%7D%5Climits%5E%5C%5E%20%2C...%2C%5Cmathop%20%7By_l%5Ek%7D%5Climits%5E%5C%5E%20%29
[theta _j]: https://private.codecogs.com/gif.latex?%7B%5Ctheta%20_j%7D
[y_j]: https://private.codecogs.com/gif.latex?%7By_j%7D
[d _ l _ 1_q _ l]: https://private.codecogs.com/gif.latex?%28d%20&plus;%20l%20&plus;%201%29q%20&plus;%20l
[q_l]: https://private.codecogs.com/gif.latex?q*l
[x_k_y_k]: https://private.codecogs.com/gif.latex?%28%7Bx_k%7D%2C%7By_k%7D%29
[E_k_ _ _frac_1_2_sum_limits_j _ 1_l _mathop _y_j_k_limits_ - y_j_k_2]: https://private.codecogs.com/gif.latex?%7BE_k%7D%20%3D%20%5Cfrac%7B1%7D%7B2%7D%5Csum%5Climits_%7Bj%20%3D%201%7D%5El%20%7B%7B%7B%28%5Cmathop%20%7By_j%5Ek%7D%5Climits%5E%5C%5E%20-%20y_j%5Ek%29%7D%5E2%7D%7D
[20190804172728361.png]: /images/20211109/dc660aa92c2844f4a0ca13f106d52ad9.png
[Delta _omega _hj_ _ - _eta _frac_partial _E_k_partial _omega _hj]: https://private.codecogs.com/gif.latex?%5CDelta%20%7B%5Comega%20_%7Bhj%7D%7D%20%3D%20-%20%5Ceta%20%5Cfrac%7B%7B%5Cpartial%20%7BE_k%7D%7D%7D%7B%7B%5Cpartial%20%7B%5Comega%20_%7Bhj%7D%7D%7D%7D
[eta]: https://private.codecogs.com/gif.latex?%5Ceta
[beta _rm_j]: https://private.codecogs.com/gif.latex?%7B%5Cbeta%20_%7B%5Crm%7Bj%7D%7D%7D
[mathop _y_j_k_limits]: https://private.codecogs.com/gif.latex?%5Cmathop%20%7By_j%5Ek%7D%5Climits%5E%5C%5E
[frac_partial _E_k_partial _omega _hj_ _ _frac_partial _E_k_partial _mathop _y_j_k_limits_ _._frac_partial _mathop _rm_y_j_k_limits_ _partial _beta _j_._frac_partial _beta _j_partial _omega _hj]: https://private.codecogs.com/gif.latex?%5Cfrac%7B%7B%5Cpartial%20%7BE_k%7D%7D%7D%7B%7B%5Cpartial%20%7B%5Comega%20_%7Bhj%7D%7D%7D%7D%20%3D%20%5Cfrac%7B%7B%5Cpartial%20%7BE_k%7D%7D%7D%7B%7B%5Cpartial%20%5Cmathop%20%7By_j%5Ek%7D%5Climits%5E%5C%5E%20%7D%7D.%5Cfrac%7B%7B%5Cpartial%20%5Cmathop%20%7B%7B%5Crm%7By%7D%7D_j%5Ek%7D%5Climits%5E%5C%5E%20%7D%7D%7B%7B%5Cpartial%20%7B%5Cbeta%20_j%7D%7D%7D.%5Cfrac%7B%7B%5Cpartial%20%7B%5Cbeta%20_j%7D%7D%7D%7B%7B%5Cpartial%20%7B%5Comega%20_%7Bhj%7D%7D%7D%7D
[frac_partial _beta _j_partial _omega _hj_ _ _b_h]: https://private.codecogs.com/gif.latex?%5Cfrac%7B%7B%5Cpartial%20%7B%5Cbeta%20_j%7D%7D%7D%7B%7B%5Cpartial%20%7B%5Comega%20_%7Bhj%7D%7D%7D%7D%20%3D%20%7Bb_h%7D
[frac_partial _mathop _rm_y_j_k_limits_ _partial _beta _j_ _ _mathop _rm_y_j_k_limits_ _1 - _mathop _rm_y_j_k_limits_]: https://private.codecogs.com/gif.latex?%5Cfrac%7B%7B%5Cpartial%20%5Cmathop%20%7B%7B%5Crm%7By%7D%7D_j%5Ek%7D%5Climits%5E%5C%5E%20%7D%7D%7B%7B%5Cpartial%20%7B%5Cbeta%20_j%7D%7D%7D%20%3D%20%5Cmathop%20%7B%7B%5Crm%7By%7D%7D_j%5Ek%7D%5Climits%5E%5C%5E%20%281%20-%20%5Cmathop%20%7B%7B%5Crm%7By%7D%7D_j%5Ek%7D%5Climits%5E%5C%5E%20%29
[beta _j]: https://private.codecogs.com/gif.latex?%7B%5Cbeta%20_j%7D
[mathop _rm_y_j_k_limits]: https://private.codecogs.com/gif.latex?%5Cmathop%20%7B%7B%5Crm%7By%7D%7D_j%5Ek%7D%5Climits%5E%5C%5E
[frac_partial _E_k_partial _mathop _y_j_k_limits_ _ _ _frac_partial _frac_1_2_sum_limits_j _ 1_l _mathop _y_j_k_limits_ - y_j_k_2_ _partial _mathop _y_j_k_limits_ _ _ _mathop _y_j_k_limits_ - y_j_k]: https://private.codecogs.com/gif.latex?%5Cfrac%7B%7B%5Cpartial%20%7BE_k%7D%7D%7D%7B%7B%5Cpartial%20%5Cmathop%20%7By_j%5Ek%7D%5Climits%5E%5C%5E%20%7D%7D%20%3D%20%5Cfrac%7B%7B%5Cpartial%20%28%5Cfrac%7B1%7D%7B2%7D%5Csum%5Climits_%7Bj%20%3D%201%7D%5El%20%7B%7B%7B%28%5Cmathop%20%7By_j%5Ek%7D%5Climits%5E%5C%5E%20-%20y_j%5Ek%29%7D%5E2%7D%7D%20%29%7D%7D%7B%7B%5Cpartial%20%5Cmathop%20%7By_j%5Ek%7D%5Climits%5E%5C%5E%20%7D%7D%20%3D%20%28%5Cmathop%20%7By_j%5Ek%7D%5Climits%5E%5C%5E%20-%20y_j%5Ek%29
[frac_partial _E_k_partial _omega _hj_ _ _mathop _y_j_k_limits_ - y_j_k_mathop _rm_y_j_k_limits_ _1 - _mathop _rm_y_j_k_limits_ _b_b]: https://private.codecogs.com/gif.latex?%5Cfrac%7B%7B%5Cpartial%20%7BE_k%7D%7D%7D%7B%7B%5Cpartial%20%7B%5Comega%20_%7Bhj%7D%7D%7D%7D%20%3D%20%28%5Cmathop%20%7By_j%5Ek%7D%5Climits%5E%5C%5E%20-%20y_j%5Ek%29%5Cmathop%20%7B%7B%5Crm%7By%7D%7D_j%5Ek%7D%5Climits%5E%5C%5E%20%281%20-%20%5Cmathop%20%7B%7B%5Crm%7By%7D%7D_j%5Ek%7D%5Climits%5E%5C%5E%20%29%7Bb_b%7D
[g_j_ _ - _frac_partial _E_k_partial _mathop _y_j_k_limits_ _._frac_partial _mathop _rm_y_j_k_limits_ _partial _beta _j_ _ - _mathop _y_j_k_limits_ - y_j_k_mathop _rm_y_j_k_limits_ _1 - _mathop _rm_y_j_k_limits_]: https://private.codecogs.com/gif.latex?%7Bg_j%7D%20%3D%20-%20%5Cfrac%7B%7B%5Cpartial%20%7BE_k%7D%7D%7D%7B%7B%5Cpartial%20%5Cmathop%20%7By_j%5Ek%7D%5Climits%5E%5C%5E%20%7D%7D.%5Cfrac%7B%7B%5Cpartial%20%5Cmathop%20%7B%7B%5Crm%7By%7D%7D_j%5Ek%7D%5Climits%5E%5C%5E%20%7D%7D%7B%7B%5Cpartial%20%7B%5Cbeta%20_j%7D%7D%7D%20%3D%20-%20%28%5Cmathop%20%7By_j%5Ek%7D%5Climits%5E%5C%5E%20-%20y_j%5Ek%29%5Cmathop%20%7B%7B%5Crm%7By%7D%7D_j%5Ek%7D%5Climits%5E%5C%5E%20%281%20-%20%5Cmathop%20%7B%7B%5Crm%7By%7D%7D_j%5Ek%7D%5Climits%5E%5C%5E%20%29
[Delta _omega _ _frac_partial _E_k_partial _omega _hj_ _ _eta _g_j_b_n]: https://private.codecogs.com/gif.latex?%5CDelta%20%5Comega%20%3D%20%5Cfrac%7B%7B%5Cpartial%20%7BE_k%7D%7D%7D%7B%7B%5Cpartial%20%7B%5Comega%20_%7Bhj%7D%7D%7D%7D%20%3D%20%5Ceta%20%7Bg_j%7D%7Bb_n%7D
[omega]: https://private.codecogs.com/gif.latex?%5Comega
[Delta _theta _j_ _ - _eta _frac_partial _E_rm_k_partial _theta _j_ _ - _eta _frac_partial _frac_1_2_sum_limits_j _ 1_l _mathop _y_j_k_limits_ - y_j_k_2_ _partial _theta _j_ _ - _eta _frac_mathop _y_j_k_limits_ - y_j_k_partial f_beta _l_ - _theta _j_partial _theta _j_ _ - _eta _ - _mathop _y_j_k_limits_ _mathop _y_j_k_limits_ - y_j_k_1 - _mathop _y_j_k_limits_ _ _ - _eta _g_j]: https://private.codecogs.com/gif.latex?%5CDelta%20%7B%5Ctheta%20_j%7D%20%3D%20-%20%5Ceta%20%5Cfrac%7B%7B%5Cpartial%20%7BE_%7B%5Crm%7Bk%7D%7D%7D%7D%7D%7B%7B%5Cpartial%20%7B%5Ctheta%20_j%7D%7D%7D%20%3D%20-%20%5Ceta%20%5Cfrac%7B%7B%5Cpartial%20%28%5Cfrac%7B1%7D%7B2%7D%5Csum%5Climits_%7Bj%20%3D%201%7D%5El%20%7B%7B%7B%28%5Cmathop%20%7By_j%5Ek%7D%5Climits%5E%5C%5E%20-%20y_j%5Ek%29%7D%5E2%7D%7D%20%29%7D%7D%7B%7B%5Cpartial%20%7B%5Ctheta%20_j%7D%7D%7D%20%3D%20-%20%5Ceta%20%5Cfrac%7B%7B%28%5Cmathop%20%7By_j%5Ek%7D%5Climits%5E%5C%5E%20-%20y_j%5Ek%29%5Cpartial%20f%28%7B%5Cbeta%20_l%7D%20-%20%7B%5Ctheta%20_j%7D%29%7D%7D%7B%7B%5Cpartial%20%7B%5Ctheta%20_j%7D%7D%7D%20%3D%20-%20%5Ceta%20%28%20-%20%5Cmathop%20%7By_j%5Ek%7D%5Climits%5E%5C%5E%20%28%5Cmathop%20%7By_j%5Ek%7D%5Climits%5E%5C%5E%20-%20y_j%5Ek%29%281%20-%20%5Cmathop%20%7By_j%5Ek%7D%5Climits%5E%5C%5E%20%29%29%20%3D%20-%20%5Ceta%20%7Bg_j%7D
[Delta _nu _ih]: https://private.codecogs.com/gif.latex?%5CDelta%20%7B%5Cnu%20_%7Bih%7D%7D
[Delta _nu _ih_ _to _alpha _h_ _to _b_h]: https://private.codecogs.com/gif.latex?%5CDelta%20%7B%5Cnu%20_%7Bih%7D%7D%20%5Cto%20%7B%5Calpha%20_h%7D%20%5Cto%20%7Bb_h%7D
[Delta _nu _ih_ _ - _eta _frac_partial _E_k_partial _nu _ih_ _ - _eta _frac_partial _E_k_partial _b_h_._frac_partial _b_h_partial _alpha _h_._frac_partial _alpha _h_partial _nu _ih]: https://private.codecogs.com/gif.latex?%5CDelta%20%7B%5Cnu%20_%7Bih%7D%7D%20%3D%20-%20%5Ceta%20%5Cfrac%7B%7B%5Cpartial%20%7BE_k%7D%7D%7D%7B%7B%5Cpartial%20%7B%5Cnu%20_%7Bih%7D%7D%7D%7D%20%3D%20-%20%5Ceta%20%5Cfrac%7B%7B%5Cpartial%20%7BE_k%7D%7D%7D%7B%7B%5Cpartial%20%7Bb_h%7D%7D%7D.%5Cfrac%7B%7B%5Cpartial%20%7Bb_h%7D%7D%7D%7B%7B%5Cpartial%20%7B%5Calpha%20_h%7D%7D%7D.%5Cfrac%7B%7B%5Cpartial%20%7B%5Calpha%20_h%7D%7D%7D%7B%7B%5Cpartial%20%7B%5Cnu%20_%7Bih%7D%7D%7D%7D
[frac_partial _alpha _h_partial _nu _ih_ _ _x_i]: https://private.codecogs.com/gif.latex?%5Cfrac%7B%7B%5Cpartial%20%7B%5Calpha%20_h%7D%7D%7D%7B%7B%5Cpartial%20%7B%5Cnu%20_%7Bih%7D%7D%7D%7D%20%3D%20%7Bx_i%7D
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MDY3MTQyNQ_size_16_color_FFFFFF_t_70 1]: /images/20211109/25dd292e60024e21bdf583d1fabb091e.png
[Delta _nu _ih_ _ _eta _e_h_x_i]: https://private.codecogs.com/gif.latex?%5CDelta%20%7B%5Cnu%20_%7Bih%7D%7D%20%3D%20%5Ceta%20%7Be_h%7D%7Bx_i%7D
[Delta _gamma _ - _eta _e_h]: https://private.codecogs.com/gif.latex?%5CDelta%20%5Cgamma%20%3D%20-%20%5Ceta%20%7Be_h%7D
[Delta _omega]: https://private.codecogs.com/gif.latex?%5CDelta%20%5Comega
[20190804174710258.png]: /images/20211109/d852e75e60fa4f899941dd07a6435a0c.png
[Delta _omega 1]: /images/20211109/59b0da85058546cca904e2029f459cc7.png
[eta 1]: /images/20211109/ead344be81474703ba9818204e3ef054.png
[E_omega]: https://private.codecogs.com/gif.latex?E%28%5Comega%20%29
[Delta _E_k_omega]: https://private.codecogs.com/gif.latex?%5CDelta%20%7BE_k%7D%28%5Comega%20%29
[Delta E_omega]: https://private.codecogs.com/gif.latex?%5CDelta%20E%28%5Comega%20%29