分类算法实例五：用KD Tree查找最近邻

野性酷女 2023-07-13 15:04 49阅读 0赞

1、KNN参数说明


































参数 K Neighbors Classifier（KNN分类）和K Neighbors Regressor（KNN回归）
weights 样本权重，可选参数: uniform（等权重）、distance（权重和距离成反比，越近影响越强）；默认为uniform
n_neighbors 邻近数目，默认为5
algorithm 计算方式，默认为auto，可选参数: auto、ball_tree、kd_tree、brute；推荐选择kd_tree
leaf_size 在使用KD_Tree的时候，叶子数量，默认为30
metric 样本之间距离度量公式，默认为minkowski（闵可夫斯基）；当参数p为2的时候，其实就是欧几里得距离
p 给定minkowski距离中的p值

2、KD Tree介绍

（1）KD Tree的适用场景
KD Tree是密度聚类（DBSCAN）算法中计算样本和核心对象之间距离来获取最近邻以及KNN算法中用于计算最近邻的快速、便捷构建方式。
当样本数据量少的时候，我们可以使用brute这种暴力的方式进行求解最近邻，即计算到所有样本的距离。但是当样本量比较大的时候，直接计算所有样本的距离，工作量有点大，所以在这种情况下，我们可以使用KD Tree来快速的计算。
（2）KD Tree的构建方式
KD树采用从m个样本的n维特征中，分别计算n个特征取值的方差，用方差最大的第k维特征 n k n_k nk​作为根节点。对于这个特征，选择取值的中位数 n k v n_{kv} nkv​作为样本的划分点，对于小于该值的样本划分到左子树，对于大于等于该值的样本划分到右子树，对左右子树采用同样的方式找方差最大的特征作为根节点，递归即可产生KD树。
（3）KD Tree示例
二维样本：{(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)}。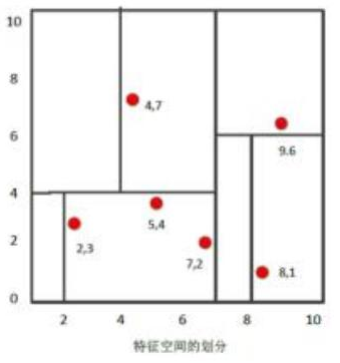
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2dvbmd4aWZhY2FpX2JlbGlldmU_size_16_color_FFFFFF_t_70
（4）KD Tree查找最近邻
当我们生成KD树以后，就可以去预测测试集里面的样本目标点了。对于一个目标点，我们首先在KD树里面找到包含目标点的叶子节点。以目标点为圆心，以目标点到叶子节点样本实例的距离为半径，得到一个超球体，最近邻的点一定在这个超球体内部。然后返回叶子节点的父节点，检查另一个子节点包含的超矩形体是否和超球体相交，如果相交就到这个子节点寻找是否有更加近的近邻,有的话就更新最近邻。如果不相交那就简单了，我们直接返回父节点的父节点，在另一个子树继续搜索最近邻。当回溯到根节点时，算法结束，此时保存的最近邻节点就是最终的最近邻。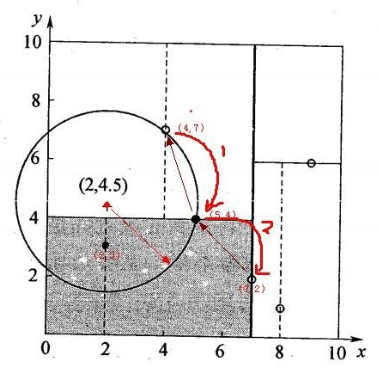
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2dvbmd4aWZhY2FpX2JlbGlldmU_size_16_color_FFFFFF_t_70 1

3、用KD Tree查找最近邻实例

  1. from sklearn.neighbors import KDTree
  2. import numpy as np
  4. np.random.seed(0)
  5. X = np.random.random((10, 3))
  6. X

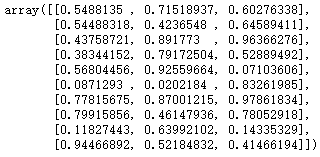
20200312214156319.png

  1. tree = KDTree(X, leaf_size=2)
  2. tree

20200312214252307.png

  1. dist, ind = tree.query([X[0]], k=3)
  2. print(dist)
  3. print(ind)

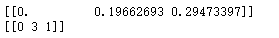
2020031221433694.png

发表评论

表情：
评论列表 （有 0 条评论，49人围观）

还没有评论，来说两句吧...

相关阅读