浅谈Huffman树-向日葵屋

浅谈Huffman树

如果要计算1~100之间，所有能被2和5整除的数的和，我们该怎么写代码？这是一个非常简单的问题，我们很快就可以写出代码：

int sum = 0; //累加的结果 
for(int i = 1; i <= 100; i++) //遍历1~100之间的数 
{
    if(i % 2 == 0) //先判断i能不能被2整除 
    {
        if(i % 5 == 0) //再判断i能不能被5整除
        {
            sum += i; //累加 
        }
    }
}
printf("sum = %d\r\n", sum); //显示结果

运行结果：
在这里插入图片描述
如果先判断能不能被5整除，然后判断是不是能被2整除，这种方式对结果没有任何影响。但是，我们要考虑一下这两种方式在效率上的差别：
第一种方式：先判断能不能被2整除，再判断能不能被5整除。
先判断能不能被2整除时，if(i % 2 == 0) 这个语句一共要执行100次，得到50个阳性结果，接着执行50次if(i % 5 == 0) 语句，得到10个阳性结果。一共判断了100 + 50 = 150次。
第二种方式：先判断能不能被5整除，再判断能不能被2整除。
先判断能不能被5整除时，if(i % 5 == 0) 这个语句一共要执行100次，得到20个阳性结果，接着执行20次if(i % 2 == 0) 语句，得到10个阳性结果。一共判断了100 + 20 = 120次。

对比这两种方式，仅仅是把2和5的次序对调一下，代码的效率就可以提高 (150 - 120) / 150 = 20%。我们把这个过程用二叉树的形式表示出来：
这两个图中只有叶子结点中有数字，这个数字表示符合指定条件的数字个数。

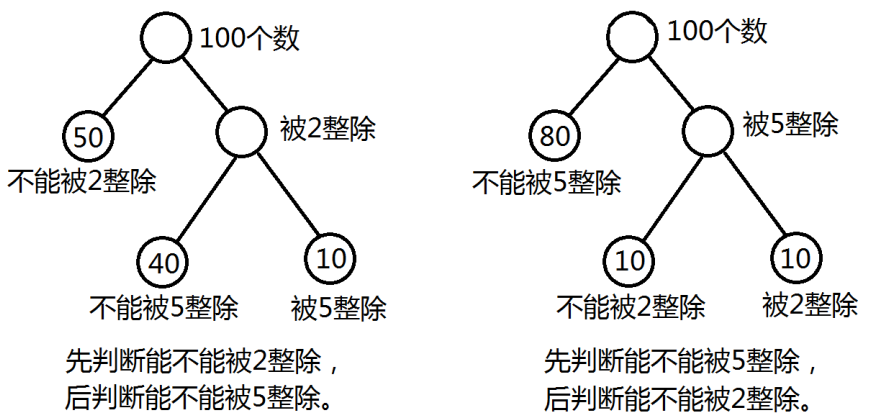
在这里插入图片描述
David Huffman (美国数学家，不要错误的写成Hoffmann) 定义：树的路径长度就是从树根到每一个叶子结点的路径的长度的和。例如左边这棵二叉树中，根节点到50的结点的长度为1，到40和10的结点的长度分别为2。所以这棵二叉树的长度为：1 + 2 + 2 = 5。这棵树的带权路径长度 (WPL) = 1 * 50 + 2 * 40 + 2 * 10 = 150。

右边的二叉树的路径长度也是5，它的带权路径长度 (WPL) = 1 * 80 + 2 * 10 + 2 * 10 = 120。
具有最小WPL值的二叉树称之为Huffman树 (也称为最优树)。显然右边的二叉树就是一棵Huffman树。

Huffman树主要用在数据压缩方面，例如Winzip、WinRar、7-Zip等压缩软件都使用了某种形式的Huffman数据压缩算法；视频网站在传输视频时，也需要把内容进行压缩。对于我们来说，我们只需要了解Huffman算法，并知道在写代码时，把能去除更多种可能的判断放在前面就可以了。这种方式在无形之中就可以提高代码的执行效率。

7 本章总结

本章介绍了树、二叉树、斜树、完全二叉树、满二叉树、二叉查找树、平衡二叉树、Huffman树等概念。介绍了树的四种遍历方式，二叉查找树的建立、查找、删除操作，介绍了一个基于树概念的算法：并查集算法。相比于之前学习的数组、链表、栈和队列来说，树这一章节的概念很多，算法也比较复杂。树这一章的内容很重要，尤其是堆 (完全二叉树的一种特殊形式)，在排序、提高查找效率等方面有重要应用。
二叉查找树相关的内容是比较复杂的，而且大量使用指针，特别是二叉查找树的删除功能。如果读者在阅读这部分内容时感觉比较吃力，可以跳过。本章最重要的是了解堆、并查集、Huffman树等概念。
树最大的价值是提高算法的效率。很多情况下，只用数组、链表、栈和队列等简单的数据结构也能完成所需的功能，但是如果在“树”上实现相同的功能，代码的效率会有明显的提升。例如并查集算法中，如果不使用路径压缩，查找老板需要遍历整个链表，时间复杂度为O(N)，但使用路径压缩技术之后，时间复杂度降低至O(1)。另一个例子是二叉查找树：在二叉查找树中添加、删除一个结点的时间复杂度为O(logN)，而在数组或链表中实现相同的功能，时间复杂度为O(N)。即使在数组中进行二分查找，使用的也是二叉查找树的搜索技术，只是平时可能没有意识到罢了。堆可能是整个章节中最重要的概念了，本章仅仅介绍了它的定义，堆主要作为堆排序、优先级队列等算法的核心数据结构，这些内容将分别在排序篇和扩展篇中介绍。