回文路径
题目出自:
codeforces Educational Codeforces Round 89 (Rated for Div. 2) C.Palindromic Paths
这个是原题链接
题目大致意思就是
给你一个矩阵
矩阵的每一个数是0或1
例如:
1 0 0 1 0 1 0
0 1 1 0 1 0 1
0 0 1 0 1 0 1
然后有个人要从左上角走到右下角
每次只能向右走或向下走一格
然后把走过的路上的数写成一行
例如:
路径为:1 0 0 1 0 1 0 1 1
如果恰好是这种左右对称的
例如:

路径为:1 0 0 1 0 1 0 0 1
那么就把它称为回文路径
题目的输入是给一个矩阵,让你输出的是,至少要改变矩阵中的多少个数,才能使每一条路径都变成回文路径
我的解法:
(先用4×6的举一下例子)
首先把每个格都做一个这样的标记(标记就是行号加列号加1)
如图:
可以发现,每条路径的第一个数都来自标记为1的格,第二个数都来自标记为2的格,第三个数都来自标记为3的格……以此类推

那么,如果要使路径为回文路径
我们需要让标记为1的数和标记为9的数相同(要么都是1,要么都是0)
需要让标记为2的和标记为8的数相同
那么问题来了
标记为2的数需不需要和另一个标记为2的数相同呢?
答案是肯定的
因为如图所示:、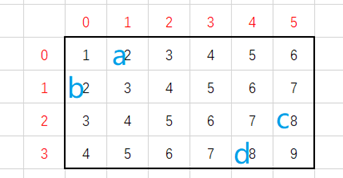
a和c必须是相同的
b和c也必须是相同的
所以a和b(两个标记为2的格)也是相同的
同理c和d(两个标记为8的格)也是相同的
所以标记为2的所有格和标记为8的所有格中的数都必须是一样的
同理标记为3的所有格和标记为7的所有格中的数都必须是一样的
同理标记为4的所有格和标记为6的所有格中的数都必须是一样的
那么问题又来了
处于回文路径最中间的标记为5的格需不需要和其他标记为5的格一样呢
显然它不需要,因为它在最中间,不管它是啥,回文路径都不会被它影响
好,那么我们得出结论
如果想让所有路径都是回文路径
我们就需要让所有i+j=k和i+j=m+n-k的格中的数相等(i是横坐标,j是列坐标,m,n是行数列数)
其中k是一个常数,k的范围是1<=k<(m+n+1)/2(因为当m+n-1为奇数时,最中间的数不用管)
那么现在我们需要计算的就是满足上述条件最少需要改变多少个数
现在我们就假如当k等于某一常数时所有i+j=k和i+j=m+n-k的格中
有a个格是0
有b个格是1
我们需要把它们都统一成0或1
如果我们把所有0都变成1
那么我们需要改变a个数
如果都变成0
我们需要改变b个数
我们需要尽可能少改变几个数
所以我们要比较一下a,b的大小
然后改变的次数就是min(a,b)
然后我们只需要把k从1到(m+n+1)/2遍历一遍,然后分别统计一下0和1的个数
再取小的那个就可以了
好,分析完了
那么代码如下:
#include <iostream>#include <cstdio>#include <cmath>#include <algorithm>using namespace std;int main(){int T;cin >> T;while (T--){int m, n; // m行数,n列数cin >> m >> n;int sz[m][n]; // s(数)z(组)// 输入for (int i = 0; i < m; i++){for (int j = 0; j < n; j++){cin >> sz[i][j];}}int sum = 0; // 要操作做次数的总数// k从1遍历到(m+n+1)/2for (int k = 1; k < (m + n + 1) / 2; k++){int a = 0, b = 0; // a储存0的个数,b储存1的个数int t = m + n - k; // t储存m+n-k// 遍历一遍数组for (int i = 0; i < m; i++){for (int j = 0; j < n; j++){if (i + j + 1 == k || i + j + 1 == t){if (sz[i][j] == 0){a++;}else{b++;}}}}// 总次数加上a,b中小的那个sum += min(a, b);}// 输出结果cout << sum << endl;}return 0;}
ヾ(≧∪≦*)ノ〃


























![[CDH] CDH5.13.1集成 Apache Spark2.3.4(CDS 2.3.4) [CDH] CDH5.13.1集成 Apache Spark2.3.4(CDS 2.3.4)](https://image.dandelioncloud.cn/images/20220225/b94aefdb8e3a46c69eb9c2a00cbf2829.png)




还没有评论,来说两句吧...