LeetCode-84. 柱状图中最大的矩形(单调栈)

POJ-2559.Largest Rectangle in a Histogram

LeetCode-84. 柱状图中最大的矩形

Description

直方图是由在公共基线处对齐的一系列矩形组成的多边形。

矩形具有相等的宽度，但可以具有不同的高度。

例如，图例左侧显示了由高度为2,1,4,5,1,3,3的矩形组成的直方图，矩形的宽度都为1：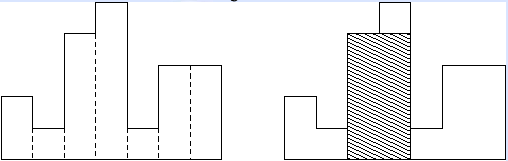
在这里插入图片描述
通常，直方图用于表示离散分布，例如，文本中字符的频率。
现在，请你计算在公共基线处对齐的直方图中最大矩形的面积。

图例右图显示了所描绘直方图的最大对齐矩形。

Input

输入包含几个测试用例。

每个测试用例占据一行，用以描述一个直方图，并以整数n开始，表示组成直方图的矩形数目。

然后跟随n个整数h1，…，hn。这些数字以从左到右的顺序表示直方图的各个矩形的高度。

每个矩形的宽度为1。同行数字用空格隔开。

当输入用例为n=0时，结束输入，且该用例不用考虑。

数据范围：

1 ≤ n ≤ 100000,

0 ≤ hi ≤ 1000000000

Output

对于每一个测试用例，输出一个整数，代表指定直方图中最大矩形的区域面积。

每个数据占一行。请注意，此矩形必须在公共基线处对齐。

Sample Input

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

Sample Output

8
4000

单调栈

我们可以维护一个单调递增的栈，当前元素比栈顶元素大或等于则直接进栈，如果当前元素比栈顶元素小，则栈顶元素出栈，直到当前元素大于或等于栈顶元素，在出栈的过程中，记录被弹出的宽度之和，并且每弹出一个矩形，就用它的高度乘上累计的宽度去更新答案。整个出栈过程结束后，把一个高度为当前矩形高度、宽度为累计值的新矩形入栈。
因为之前比它高度小的矩形都出栈了，所以需要累计比它小的宽度和。
整个扫描结束后，把栈中剩余的矩形依次弹出，用同样的方法，也可以增加一个高度为0的矩形，来避免在扫描结束后栈中有剩余矩形。

LeetCode

class Solution { 
public:
    int largestRectangleArea(vector<int>& heights) { 
        int ans=0;
        vector<int> w(heights.size()+1,1);
        vector<int> vec(heights);
        vec.push_back(0);
        stack<int> st;
        for(int i=0;i<vec.size();i++)
        { 
            int width=0;
            while(!st.empty()&&vec[st.top()]>vec[i])
            { 
                width+=w[st.top()];
                ans=max(ans,width*vec[st.top()]);
                st.pop();
            }
            st.push(i);
            w[i]=width+1;
        }
        return ans;
    }
};

Poj

#include <iostream>
#include <algorithm>
#include <stack>
#include <vector>
using namespace std;
long long ans = 0;
int a[100010];
int w[100010];
int n;
stack<int> st;
int main()
{ 
    while (cin >> n && n)
    { 
        ans = 0;
        fill(w, w + n + 1, 1);
        while (!st.empty()) //栈清空
            st.pop();
        for (int i = 0; i < n; i++)
        { 
            cin >> a[i];
        }
        a[n] = 0;
        for (int i = 0; i <= n; i++)
        { 
            int width = 0; //记录被弹出矩形的宽度和
            while (!st.empty() && a[st.top()] > a[i])
            { 
                width += w[st.top()];
                ans = max(ans, (long long)a[st.top()] * width);
                st.pop();
            }
            w[i] = width + 1; //更新宽度
            st.push(i);
        }
        cout << ans << endl;
    }
    return 0;
}