草原火势-林火蔓延模型原理及GIS应用示例-向日葵屋

草原火势-林火蔓延模型原理及GIS应用示例

清疚 2024-04-08 11:55 43阅读 0赞

1 在线模拟示例

在线模拟示例

加入了道路，水系，村庄等无法燃烧的地表覆盖类型的影响计算。例如高速公路可以阻断火势的传播，而火势可以绕过村庄和湖库继续传播

2 林火蔓延介绍

本文基于王正非林火蔓延模型，采取元胞自动机的算法模拟林火蔓延过程，通过地图实现地形和林火的显现，实现在模拟的地图环境中，根据气象、地形、植被因素的不同模拟林火的发生发展状态，通过三维模拟林火的发生发展、预判其发展态势，对组织指挥扑救，提高灭火效率和确保灭火人员安全具有一定参考意义。

3 元胞及其状态

3.1 元胞及其邻域

在 Moore型邻居邻居中，一个元胞的上、下、左、右4个相邻元胞( adjacent neighbor cells）加上对角线方向上的4个次相邻元胞（diagonal neighbor cells）为该元胞的邻居。如图3-1，邻胞即与中心元胞(i,j)有公共边的元胞,分别用(i-1, j)，(i+l, j)，(i,j-1)，(i, j+1)表示。次邻元胞即位于对角线方向上的4个位置,分别用(i-1,j-l)， (i一1,j+l), (i+1,j-l)，(i+1, j+1)表示。

3.1 元胞及其状态

t时刻元胞(i,j)的状态定义为:

$^\{A\{ij\}^\{t\}\}$ 的取值范围是:0≤ $^\{A\{ij\}^\{t\}\}$ ≤1。如果 $^\{A\{ij\}^\{t\}\}$ =0，表示在t时刻元胞(i,j)未燃烧;0< $^\{A\{ij\}^\{t\}\}$ <1表示表示在t时刻元胞(i,j)部分燃烧; $^\{A\{ij\}^\{t\}\}$ =1表示在t时刻元胞(i,j)完全燃烧，假设只有完全燃烧的元胞才会对邻域元胞进行火蔓延。
在此基础上，可以根据实际情况增加相应的状态表达。如在进行机上模拟实验的时，由于模拟需要，当 $^\{A\{ij\}^\{t\}\}$ =1的后的t+1时刻开始可以置元胞的状态为2，表示该元胞已经完全燃烧，从t+1时刻开始向周围的元胞蔓延；另外我们可以置邻域元胞已经完全燃烧的元胞状态为3，表示该元胞已经熄灭。

4 模拟流程

1、模拟点火，将当前元胞状态赋值为2；

2、根据模拟总时长和步长（单次时长）进行循环计算：计算么着火点的8个邻域，计算淋雨的着火面积；将完全着火的点状态赋值为2；将邻域元胞完全燃烧的元胞状态赋值为3

3、将所有元胞进行汇总，生成空间数据要素层，返回客户端。

5 参数变量

王正非提出的林火蔓延速度计算方程如下:

5.1 初始蔓延速度R

王正非导出的初始蔓延速度回归式为:

5.2 Ks是可燃物配置格局更正系数

K,用来表征可燃物的易燃程度(化学特性)及是否有利于燃烧的配置格局(物理特性)的一个更正系数,对某时、某地来说，整个燃烧范围和燃烧过程中，K,可以假定为常数。王正非按照野外实地可燃物配置类型，把它予以参数化。

5.3 Kw是风速调整系数

众所周知，在一定范围内，风速V越大，风方向上的蔓延速度越大，即风引起的增益
值Kw也越大，王正非提供了一个Kw，随着风速V变化的实验数据表。

地形坡度调整系数" class="reference-link">5.4 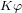$^\{K\{\\varphi \}\}$ 地形坡度调整系数

综合上述，可以写出经毛贤敏改进后的林火蔓延速度的基本公式：

6 关键技术点

1、后端技术栈推荐：ArcGIS、SuperMap二次开发组件；GeoTools+JTS；有条件可使用GDAL。

2、坐标转换：前端一般是经纬度坐标，在后端应进行精确投影，毕竟高斯模拟的条件是10km范围内。

3、主要模拟结果，火势一般是往上坡走

7 参考代码

获取邻近元胞：

private CellNeighborsGroup getCellNeighborsGroup(Cell curCell) {
        CellNeighborsGroup neighborsGroup = new CellNeighborsGroup(this.winSize);
        int m = curCell.getM();
        int n = curCell.getN();
        //中心元胞
        neighborsGroup.getGroup()[1][1] = new CellNeighbors(new Cell(m, n), this.winSize);
        //上面的元胞
        neighborsGroup.getGroup()[0][1] = new CellNeighbors(new Cell(m, n + this.cellSize), this.winSize);
        //下面的元胞
        neighborsGroup.getGroup()[2][1] = new CellNeighbors(new Cell(m, n - this.cellSize), this.winSize);
        //左边的元胞
        neighborsGroup.getGroup()[1][0] = new CellNeighbors(new Cell(m - this.cellSize, n), this.winSize);
        //右边的元胞
        neighborsGroup.getGroup()[1][2] = new CellNeighbors(new Cell(m + this.cellSize, n), this.winSize);
        //左上的元胞
        neighborsGroup.getGroup()[0][0] = new CellNeighbors(new Cell(m - this.cellSize, n + this.cellSize), this.winSize);
        //右上的元胞
        neighborsGroup.getGroup()[0][2] = new CellNeighbors(new Cell(m + this.cellSize, n + this.cellSize), this.winSize);
        //左下的元胞
        neighborsGroup.getGroup()[2][0] = new CellNeighbors(new Cell(m - this.cellSize, n - this.cellSize), this.winSize);
        //右下的元胞
        neighborsGroup.getGroup()[2][2] = new CellNeighbors(new Cell(m + this.cellSize, n - this.cellSize), this.winSize);
        return neighborsGroup;
    }